About

Accurate and stable numerical simulation of transient wave propagation is a fundamental requirement in geotechnical earthquake engineering and related fields. The finite element method (FEM) is widely used for this purpose; however, its classical semidiscrete formulation, in which FEM is applied only in space and the resulting system of ordinary differential equations is solved using finite difference–based time integration schemes, suffers from inherent limitations. In particular, the temporal accuracy of semidiscrete FEM is typically restricted to second order, and numerical dispersion and spurious oscillations may become significant in long-duration simulations, especially when higher-order spatial elements are employed.

This webinar presents a comprehensive overview of the space–time finite element method (ST/FEM) as an effective framework for overcoming these limitations. In ST/FEM, FEM is applied consistently in both space and time, allowing the use of arbitrary higher-order interpolation in the space–time domain. As a result, higher-order spatial elements can be naturally combined with higher-order time approximation, enabling improved accuracy and enhanced control over numerical dispersion.

The presentation begins with a conceptual comparison between semidiscrete FEM and ST/FEM, emphasizing that the two approaches are identical up to spatial discretization and differ only in the treatment of the temporal domain. The formulation of ST/FEM is then introduced, including the interpolation of field variables in time, the role of velocity and displacement shape functions, and the structure of the resulting space–time matrix–vector system.

The numerical properties of ST/FEM are examined in detail through spectral analysis. It is shown that the method is unconditionally stable and that the dissipation of high-frequency components can be controlled by a user-defined parameter, α. The influence of α on numerical damping, bifurcation behavior, and high-frequency attenuation is discussed, with particular emphasis on its relevance to geotechnical earthquake engineering problems, where suppression of spurious high-frequency oscillations is often desirable.

Accuracy is assessed through relative phase speed error (RPSE) analysis. The results demonstrate that ST/FEM exhibits significantly lower frequency errors than semidiscrete time integration schemes and achieves higher-order accuracy in time, even for linear time interpolation. The combined effects of spatial and temporal discretization are analyzed using RPSE contour plots, highlighting the dependence of dispersion errors on space–time order and CFL number, and providing practical guidance for selecting appropriate discretization parameters.

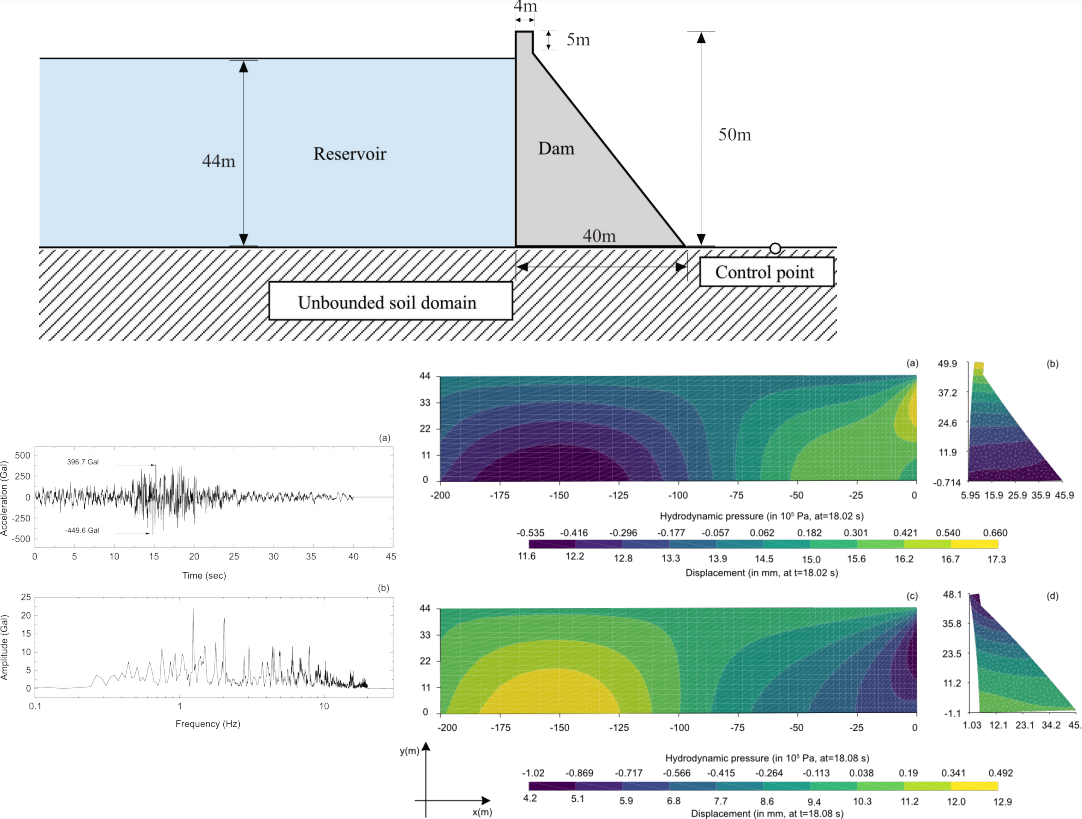
Several numerical examples, including one-dimensional and two-dimensional wave propagation problems, are presented to illustrate the performance of ST/FEM. These examples demonstrate the method’s ability to suppress head and tail oscillations, reduce anisotropic dispersion errors, and deliver nearly oscillation-free solutions when higher-order spatial elements are employed.

The webinar concludes with a discussion of the current state of ST/FEM research, its implementation using open-source tools, and future research directions, including the development of efficient solvers and extended dispersion analyses for higher-order space–time elements.